Click or Tap the Example circuits below to invoke TINACloud and select the Interactive DC mode to Analyze them Online. Get a low cost access to TINACloud to edit the examples or create your own circuits
WYE to DELTA and DELTA to WYE CONVERSION 
CURRENT DIVISION
A series connected circuit is often referred to as a voltage divider circuit. The source voltage equals the total of all voltage drops across the series connected resistors. The voltage dropped across each resistor is proportional to the resistance value of that resistor. Larger resistors experience larger drops, while smaller resistors experience smaller drops. The voltage divider formula allows you to calculate the voltage drop across any resistor without having to first solve for the current. The voltage divider formula is:
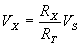
where VX = voltage dropped across selected resistor
RX = selected resistor’s value
RT = total series circuit resistance
VS = source or applied voltage
A simple example to start:
Example 1
Find the voltage drop across each resistor, given that V=150 V, R = 1 Kohm.
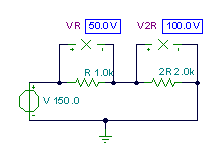
The first solution requires that we find the series current. First, calculate the circuit’s total resistance: Rtot = R1 + R2 = 1k+2k = 3 kohm.
Next, find the circuit current: I = V/Rtot = 150/3 = 50 mA.
Finally, find the voltage across R1: V1= I R1 = 50 V;
and the voltage across R2: V2 = I R2 = 100 V.
The second, more direct solution uses the voltage divider formula:
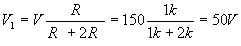
and
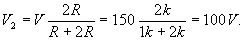
I:=V/(R+2*R);
VR:=I*R;
V2R:=I*2*R;
VR=[50]
V2R=[100]
{or using the voltage divider formula:}
VR:=V*R/(R+2*R);
V2R:=V*2*R/(R+2*R);
VR=[50]
V2R=[100]
I= V/(R+2*R)
VR= int(I*R)
V2R= int(I*2*R)
print(“Using Ohm’s Law:”)
print(“VR= %.3f”%VR, “\n”, “V2R= %.3f”%V2R)
VR= int(V*R/(R+2*R))
V2R= int(V*2*R/(R+2*R))
print(“Or using the Voltage Divider formula:”)
print(“VR= %.3f”%VR, “\n”, “V2R= %.3f”%V2R)
Another example:
Example 2
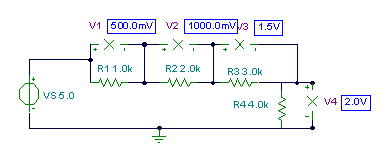
Find the voltage drop on each resistors.
Use the voltage divider formula:
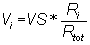
{Use the voltage divider formula: Vi= Vs*Ri/Rtot}
V1:=VS*R1/(R1+R2+R3+R4);
V2:=VS*R2/(R1+R2+R3+R4);
V3:=VS*R3/(R1+R2+R3+R4);
V4:=VS*R4/(R1+R2+R3+R4);
V1=[500m]
V2=[1]
V3=[1.5]
V4=[2]
Rtot=R1+R2+R3+R4
V1= VS*R1/Rtot
V2= VS*R2/Rtot
V3= VS*R3/Rtot
V4= VS*R4/Rtot
print(“V1= %.3f”%V1)
print(“V2= %.3f”%V2)
print(“V3= %.3f”%V3)
print(“V4= %.3f”%V4)
Example 3
Find the voltages measured by the instruments.
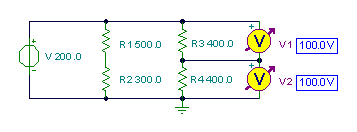
This example shows that the branch connected in parallel with the source does not affect the use of the voltage division formula.
V1:=V*R3/(R3+R4);
V1=[100]
V2:=V*R4/(R3+R4);
V2=[100]
V1=V*R3/(R3+R4)
print(“V1= %.3f”%V1)
V2=V*R4/(R3+R4)
print(“V2= %.3f”%V2)
The following example is a bit more complicated:
Example 4
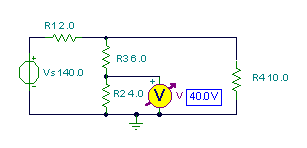
Find the voltage drop across R2 if the voltage source is 140 V and the resistances are as given in the schematic.
V4:=Vs*(Replus(R4,(R2+R3)))/(R1+Replus((R2+R3),R4));
V:=V4*R2/(R2+R3)
{or}
Sys I,I2,I1,V
I*R4=I2*(R2+R3)
I1=I+I2
V=I2*R2
Vs=R1*I1+I*R4
end;
V=[40]
Replus= lambda R1, R2 : R1*R2/(R1+R2)
V4=Vs*Replus(R4,R2+R3)/(R1+Replus(R2+R3,R4))
V2=V4*R2/(R2+R3)
print(“V2= %.3f”%V2)
The voltage division formula is used twice, first to find the voltage across R4, and second to find the voltage across R2.
Example 5
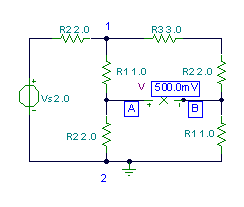
Find the voltage between the nodes A and B.
Use the voltage division formula three times:
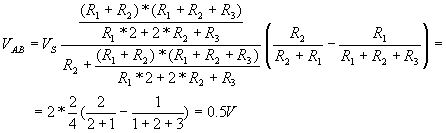
The method here is to first find the voltage between the ground node and the node (2) where R2, R3, and R1 are joined. This is done using the voltage divider formula to find the portion of Vs appearing between these two nodes. Then the voltage divider formula is used twice to find Va and Vb. Finally, Vb is subtracted from Va.
R12:=Replus((R1+R2),(R1+R2+R3));
V12:=Vs*R12/(R2+R12);
Vab:=V12*(R2/(R1+R2)-R1/(R1+R2+R3));
Vab=[500m]
Replus= lambda Ro, Rt : Ro*Rt/(Ro+Rt)
R12=Replus(R1+R2,R1+R2+R3)
V12=Vs*R12/(R2+R12)
Vab=V12*(R2/(R1+R2)-R1/(R1+R2+R3))
print(“Vab= %.3f”%Vab)
English
German
French
Spanish
Portuguese
Russian
Chinese (Simplified)
Chinese (Traditional)
Japanese
Korean
Hungarian