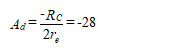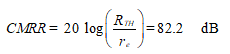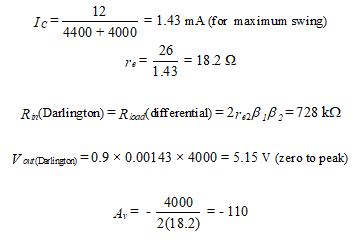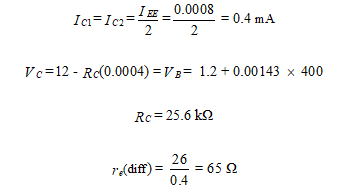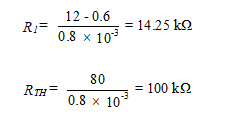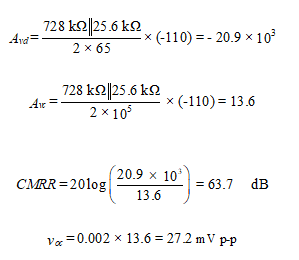Differential Amplifiers-TINA and TINACloud Resources

Differential Amplifiers

Most operational amplifiers are comprised of a series of transistors, resistors, and capacitors forming a complete system on a single chip. The amplifiers available today are reliable, small in size, and consume very little power.

The input stage of most op-amps is a Differential Amplifier as shown in its simplest form in Figure 1.

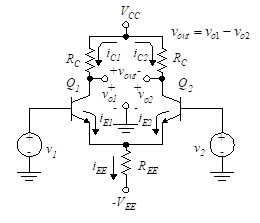
Differential Amplifiers, Practical operational amplifier, circuit simulation, circuit simulator, circuit design,

Figure 1 – Differential amplifier

The differential amplifier is composed of two emitter-coupled common-emitter dc amplifiers. It has two inputs, v₁ and v₂, and three outputs, v_o1, v_o2 and v_out. The third output, v_out, is the difference between v_o1 and v_o2.

1.1 dc Transfer Characteristics

The differential amplifier does not operate linearly with large signal inputs. In order to simplify the analysis we assume that RE is large, that the base resistance of each transistor is negligible and that the output resistance of each transistor is large. Note that we use REE rather than RE in the differential amplifier since the resistor used here is large and may be the equivalent resistance of a current source. The large value of REE keeps the emitter resistor voltage drop nearly constant.
We now solve this circuit for the output voltage. We begin by writing a KVL equation around the base junction loop for the circuit of Figure 1.

(1)

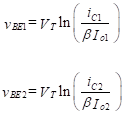
(2)

We need to find expressions for the collector currents, i_C1 and i_C2. The base-emitter voltages are given by the equation,

In Equation (2) I_o1 and I_o2 are the reverse saturation currents for Q₁ and Q₂ respectively. The transistors are assumed to be identical. Combining Equations (1) and (2) yields

(3)

Solving Equation (3) for the current ratio, we find,

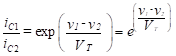
(4)

We can assume i_C1 is approximately equal to i_E1 and i_C2 is approximately equal to i_E2. Therefore

(5)

Combining Equations (4) and (5) , we have

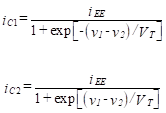
(6)

Note that

(7)

An important observation can be made by viewing Equation (6) . If v₁– v₂ becomes greater than several hundred millivolts, the collector current in transistor 2 becomes small and the transistor is essentially cut off. The collector current in transistor 1 is approximately equal to i_EE, and this transistor is saturated. The collector currents, and therefore the output voltage v_out, become independent of the difference between the two input voltages.

Linear amplification occurs only for input voltage differences less than approximately 100 mV. In order to increase the linear range of the input voltage, small emitter resistors can be added.

1.2 Common-Mode and Differential-Mode Gains

The differential amplifier is intended to respond only to the difference between the two input voltages, v₁ and v₂. However, in a practical op-amp the output depends to some degree on the sum of these inputs. For example, if both inputs are equal, the output voltage should ideally be zero, but in a practical amplifier it is not. We label the case when the circuit responds to the difference as the differential mode. If the two inputs are made equal, we say the circuit is in its common mode. Ideally we would expect the circuit to produce an output only in the differential mode.

Any two input voltages, v₁ and v₂, can be resolved into a common and a differential part. We define two new input voltages as follows:

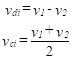
(8)

The voltage, v_di, is the differential-mode input voltage and it is simply the difference between the two input voltages. The voltage, v_ci, is the common-mode input voltage, and it is the average of the two input voltages. The original input voltages can be expressed in terms of these new quantities as follows:

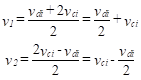
(9)

If we set the two input voltages equal, we have

(10)

Since the two inputs are equal, the emitter-base junction voltages are equal (if the transistors are identical). Thus, the collector currents must also be identical.

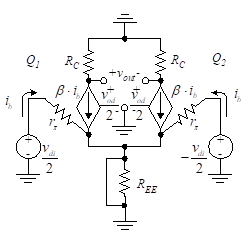
Differential Amplifiers, circuit simulation, circuit simulator, circuit design, practical op-amps

Figure 2(a) Differential-mode amplifier equivalent circuit

We now view the equivalent circuit for the differential-mode input voltage as shown in Figure 2(a). Note that as the current in the Q₁ circuit increases, the current in the Q₂ circuit decreases at the same rate and amplitude. This is true since the input to Q₂ is equal to that of Q₁ but 180^o out of phase. Thus the voltage change across R_EE is zero. Since the ac signal voltage across R_EE is zero, it can be replaced by a short circuit in the ac equivalent circuit. Note that placing voltages at each transistor base which are equal in amplitude but 180^o out of phase is equivalent to placing a voltage between the two transistor bases of twice the amplitude. The voltages at v_o1 and v_o2 are of equal amplitude but opposite phase and the differential-mode gain is

(11)

This differential-mode gain is defined at a single-ended output since it is taken between one collector and ground. If the output is taken between v_o1 and v_o2, the differential-mode gain is termed a double-ended output and is given by

(12)

A similar analysis can be applied to the common-mode equivalent circuit in Figure 2(b).

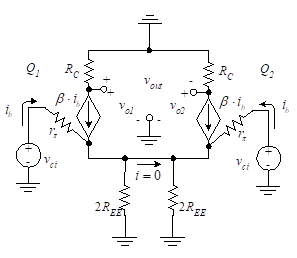
Figure 2(b) Common-mode amplifier equivalent circuit

If we divide the resistor R_EE into two parallel resistors each having double the original resistance, we can find the output by analyzing only half of the circuit. Since the transistors are identical and the common-mode input voltages are equal and in-phase, the voltages across the 2R_EE resistors are the same. Thus, the current between the two parallel resistors shown for is zero and we need only look at one side of the circuit. The common-mode voltage gain is then

(13)

Equation (13) assumes R_EE is large and r_e<<R_EE.

We find the double-ended output voltage in terms of the common-mode and differential-mode gain as follows:

(14)

It is desirable for the differential-mode gain to be much larger than the common-mode gain so that the amplifier reacts primarily to the difference between the input voltages. The common-mode rejection ratio, CMRR, is defined as the ratio of the differential-mode gain to the common-mode gain. It is usually expressed in dB.

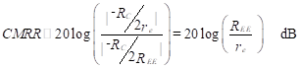
(15)

We now determine the input resistance of the amplifier in both the differential mode and the common mode. For the differential mode, we look into the amplifier at the base of both transistors. This results in a complete circuit through the emitter of both transistors, and the input resistance is

(16)

Now for the common-mode input, we look into the amplifier in Figure 2(b). Thus, the input resistance is

(17)

These results indicate that the input resistance of the common mode is much higher than that of the differential mode.

Our differential amplifier analysis is based upon BJTs as the transistor building blocks. FETs can also be used in differential amplifiers with the resulting advantages of reduced input bias current and nearly infinite input impedance. The analysis of the differential amplifier using FETs is accomplished in the same way as that of BJT analysis.

Differential amplifiers need matched transistors to insure that the circuit operates correctly. If the differential amplifier is on an integrated circuit, this additional requirement is less of a problem since the two transistors are fabricated at the same time using the same material.

1.3 Differential Amplifier with Constant Current Source

It is desirable to make R_EE as large as possible in order to reduce the common-mode output. Equation shows that to make the CMRR large we must make R_EE large. Since large resistances are hard to fabricate on IC chips, we seek an alternate approach. This is accomplished by replacing R_EE with a dc current source. An ideal current source has infinite impedance, so we investigate the possibility of replacing R_EE with such a current source. Figure 9.3 illustrates a differential amplifier where the resistor, R_EE, is replaced with a constant-current source.

(18)

The closer the source is to the ideal constant-current source, the higher the common-mode rejection ratio. We illustrate a diode-compensated fixed-bias current source. The compensation makes the operation of the circuit less dependent on temperature variations. Diode D₁ and transistor Q₃ are selected so that they have nearly identical characteristics over the range of operating temperatures.
In order to analyze the circuit of Figure 3(a) and find the CMRR, we need to determine the equivalent resistance, R_TH (the Thevenin equivalent of the constant current source circuit). The equivalent resistance is given by [see Figure 3(b)]

Writing a KCL equation at node 1, we have

(19)

where r_o is the internal resistance of the transistor at the specified operating point. It is given by

(20)

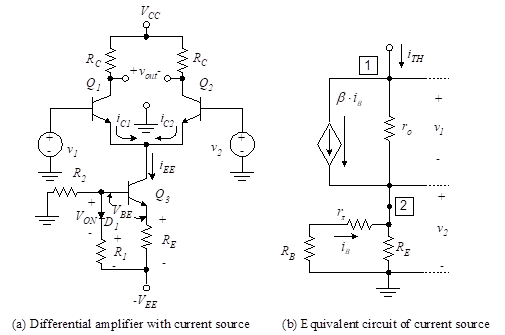
Differential Amplifiers, circuit simulation, circuit simulator, circuit design, practical op-amps

Figure 3 – Differential amplifier with constant-current source

A KCL equation at node 2 yields

(21)

where

(22)

Substituting v₁ and v₂ into the equation at node 2, we have

(23)

Finally, the Thevenin resistance is given by substituting Equations (22) and (23) into Equation (18) .

(24)

We will now make a series of assumptions to greatly simplify this expression. To maintain bias stability, we use the guideline that

(25)

Substituting this value of R_B in Equation (24) and dividing by β, we have

(26)

We can simplify this expression by noting

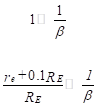
(27)

We then have

(28)

Since the second term in this equation is much greater than the first, so we can ignore R_E to obtain

(29)

This equation can be further simplified if the following condition exists:

(30)

In that case, we have the simple result

(31)

Hence, if all of the approximations are valid, R_TH is independent of β and its value is quite large.

1.4 Differential Amplifier with Single-Ended Input and Output

Figure 4 shows a differential amplifier where the second input, v₂, is set equal to zero and the output is taken as v_o1.

We use a constant current source in place of R_EE, as discussed in the previous section. This is known as a single-ended input and output amplifier with phase reversal. The amplifier is analyzed by setting v₂= 0 in the earlier equations. The differential input is then simply

(32)

so the output is

(33)

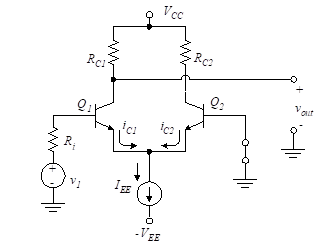
Figure 4 – Single-ended input with phase reversal

The minus sign indicates that this amplifier exhibits an 180^o phase shift between the output and input. A typical sinusoidal input and output are illustrated in Figure 5.

Figure 5 – Sinusoidal input and output

If an output signal is to be referenced to ground but a phase reversal is not desired, the output can be taken from transistor Q₂.

Example 1 – Differential Amplifier (Analysis)

Find the differential voltage gain, the common-mode voltage gain, and the CMRR for the circuit shown in Figure 1. Assume that R_i = 0, R_C = 5 kΩ, V_EE= 15 V, V_BE= 0.7 V, V_T= 26 mV, and R_EE = 25 kΩ. Let v₂ = 0 and take the output from v_o2.

Solution: The current through R_EE is found at the quiescent condition. Since the base of Q₂ is grounded, the emitter voltage is V_BE = 0.7 V, and

The quiescent current in each transistor is one-half of this amount.

Since

the differential voltage gain in each transistor is

The common-mode voltage gain is

The common-mode rejection ratio is then given by

APPLICATION

Also, you can carry out these calculations with TINA or TINACloud circuit simulators, using their Interpreter tool by clicking the link below.

1- Differential Amplifier Circuit Simulation

Example 2

For the differential amplifier described in Example 1, design a temperature-compensated fixed-bias current source (Figure 3) to replace R_EE and determine the new CMRR for the differential amplifier, with r_o = 105 kΩ, V_BE = 0.7 V, and β = 100. Assume R₁ = R₂.

Solution: We place the transistor operating point in the middle of the dc load line.

Then, referring to the current source of Figure 3(a),

For bias stability,

Then

Since 0.1R_E>>r_e (i.e., 1.25 kΩ >> 26/0.57 Ω), then from Equation (31) we have

The CMRR is given by

APPLICATION

Also, you can carry out these calculations with TINA or TINACloud circuit simulators, using their Interpreter tool by clicking the link below.

2- Differential Amplifier Circuit Simulation

Example 3

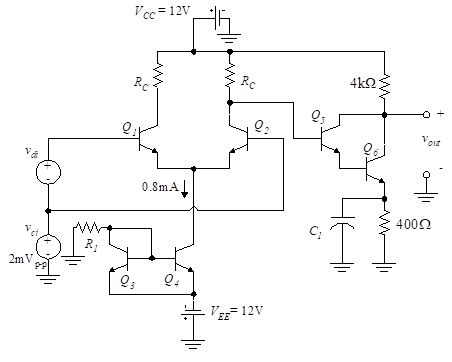
Design a circuit to attain the conditions as specified in Figure 6 for maximum output voltage swing. The five transistors, Q₁ to Q₅, each have β = 100 while Q₆ has a β of 200. V_BE is 0.6 V for all transistors, V_T= 26 mV, and V_A= 80 V. Assume all transistors are identical.